[コンプリート！] 平行四辺形 対角線 長さ ベクトル 621724
平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ
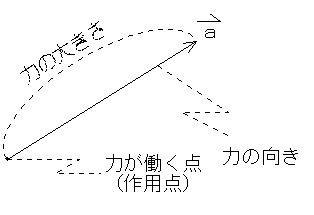
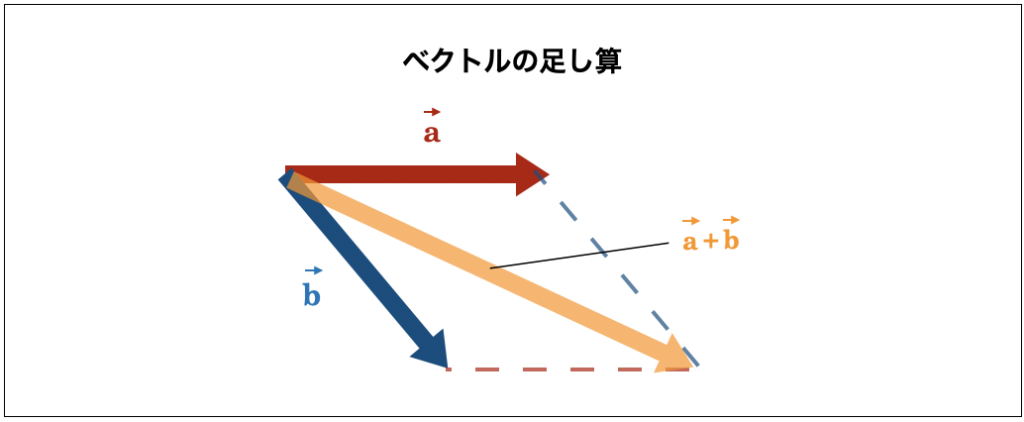
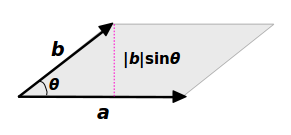
ベクトル積の大きさは平行四辺形の面積 ここでは ベクトル積 (クロス積、外積) の大きさは、2 つのベクトルが作る平行四辺形の面積に等しい ということについて説明します。 以前の説明 ではベクトル a → \overrightarrow {a} a と b → \overrightarrow {b} b が ベクトルの 和 は、ベクトルの始点を揃えて 平行四辺形 を作る。 その対角線がベクトルの和である。 ベクトルの 差 は 引く側のベクトルを逆にして足す;
平行四辺形 対角線 長さ ベクトル
平行四辺形 対角線 長さ ベクトル- ベクトルの分野では、"矢印"を扱うためのルールを学びます。そのルールを理解すれば、後はちょっとしたコツで、図形や座標・方程式の問題を簡単に解くことができるようになります。ここでは ベクトルとはなにか？ ベクトルの扱い方・ルール ベクト平行四辺形の定義と性質をまとめると以下の通り。 平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理（性質） 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう
仕事 側 ファインド 平行四辺形 不足分 Rectangle より小さい 角度 問題 対角線 同輩 60 Parallelograms 不足分 交差しなさい 見つけること ８ 幾何学的 Degrees Canstock
平行四辺形 abcd と対角線の交点 o ベクトルで計算するだけで、線分が平行であることや線分の長さが等しいことがわかるんですね。 ここでは、平行四辺形を使って、ベクトルの演算を見てきました。1つのベクトルから、しりとりができるように間に点 こんにちは、ウチダです。 今日は、中学 $2$ 年生の内容である 「平行四辺形になるための $5$ つの条件」 について、平行四辺形の定義から性質を証明し、そのあとで性質と条件が具体的にどう違うのかを詳しく見ていきましょう。 平行四辺形の定平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a b
四辺形の対角線qlq3に 平行で,長 さがこの対角線 の長さの1/2で あるまた,p1で の2階 微分ベクトルは 同一の平行四辺形の対角線ベクトルq2d1に 等しい 同様に,1本 目の曲線の終点p2で も平行辺角形 三角形の \(2\) 辺の中点を結んだ線分は残りの \(1\) 辺と平行で、長さはその半分となります。 実は、よく見てみると \(\triangle \mathrm{AMN}\) と \(\triangle \mathrm{ABC}\) は 相似比が \(\bf{1 2}\) の相似な図形 となっています。 そのことをあわせて理解しておくと、定理を忘れてしまっても思い出せますよ！ 数学・算数 ベクトルの問題なのですが 四角形abcdは平行四辺形ではなく、かつab=bcである。 辺AB，CDの中点をそれぞれP，Q
平行四辺形 対角線 長さ ベクトルのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |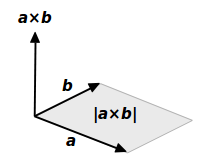
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 | 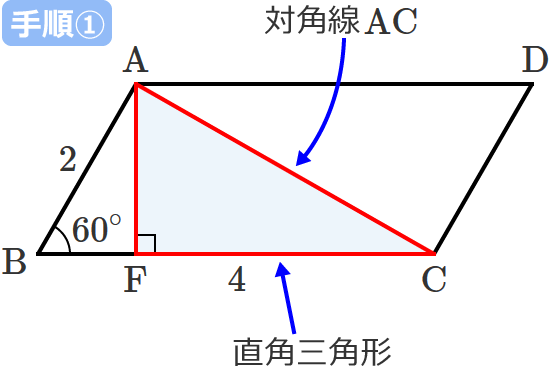 ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 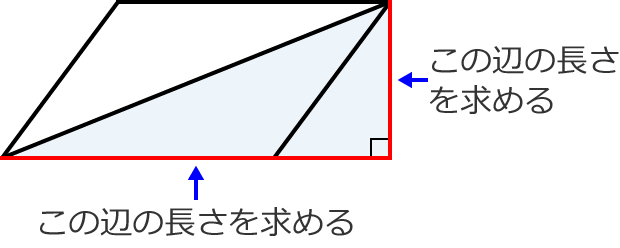 ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 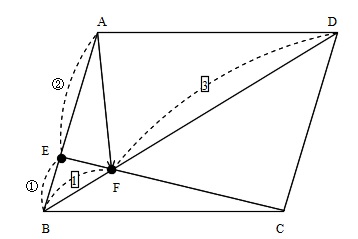 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 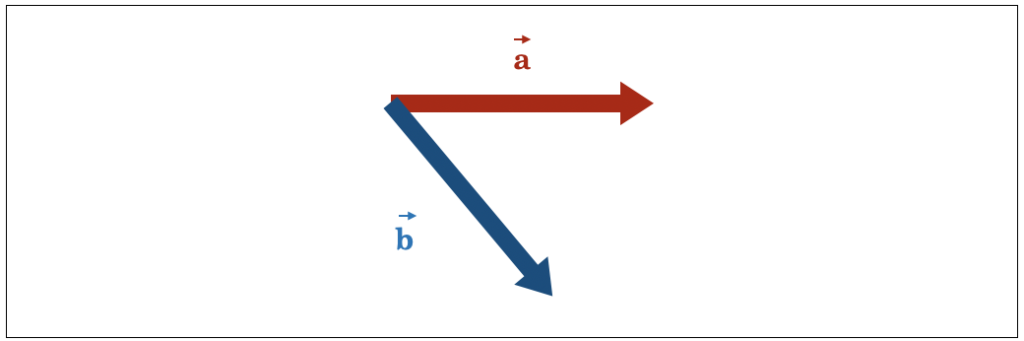 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 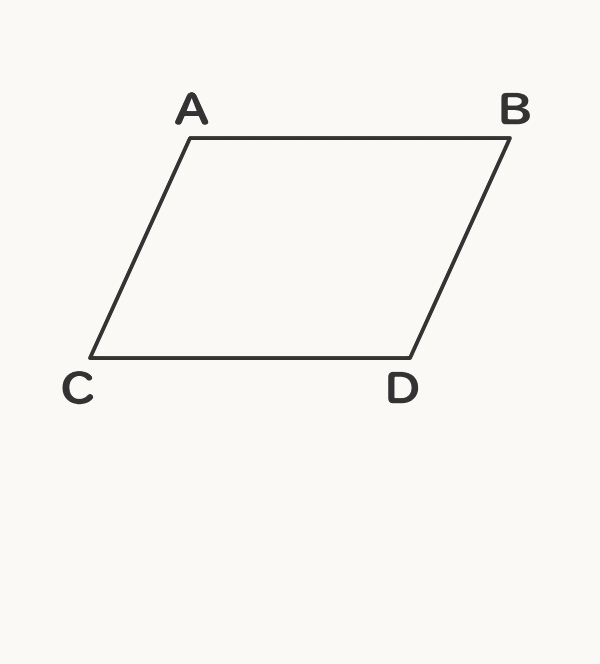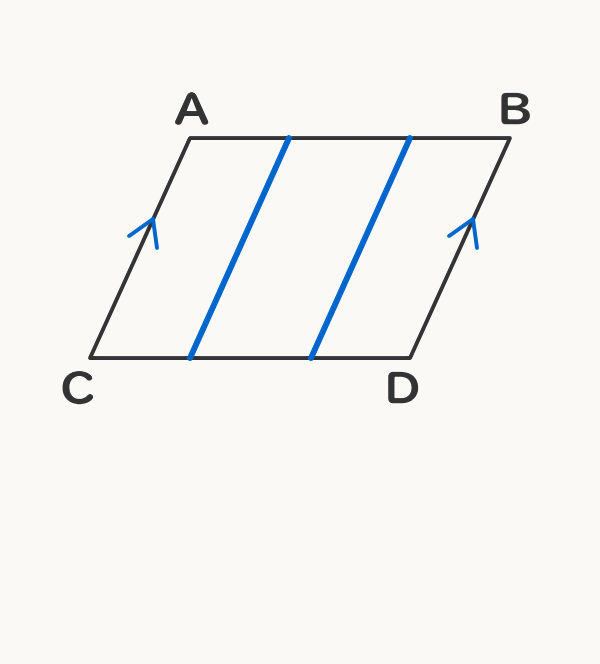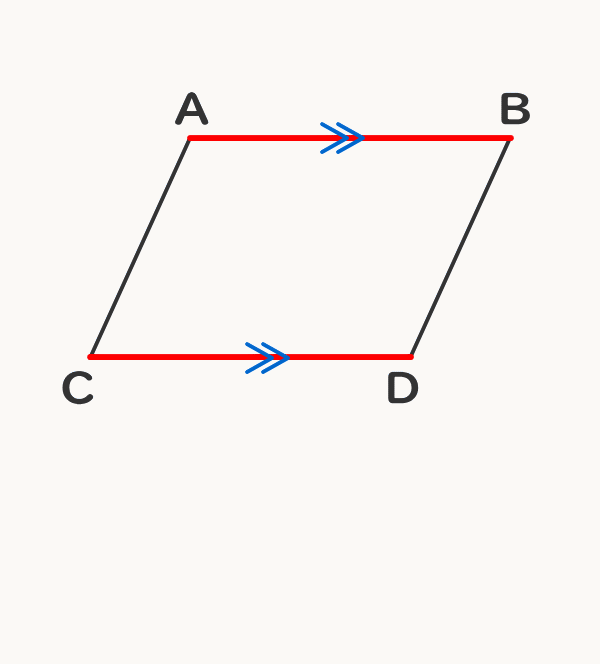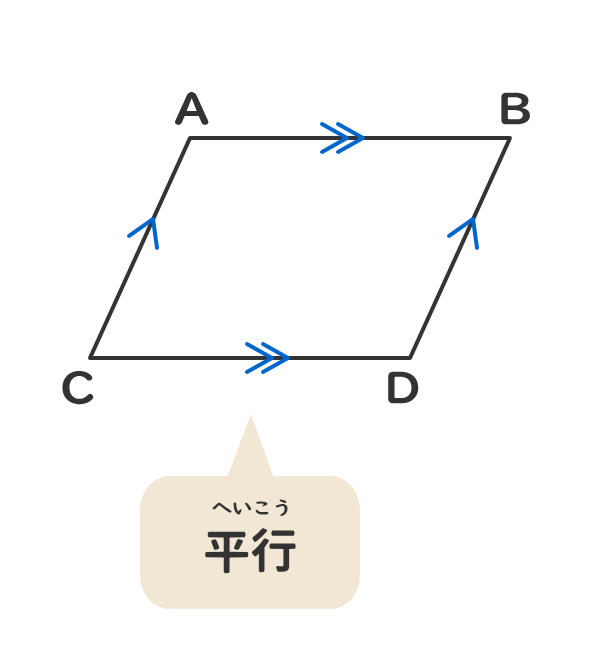 ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |
ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 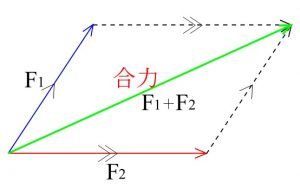 ベクトルの外積と平行四辺形の面積 身勝手な主張 | 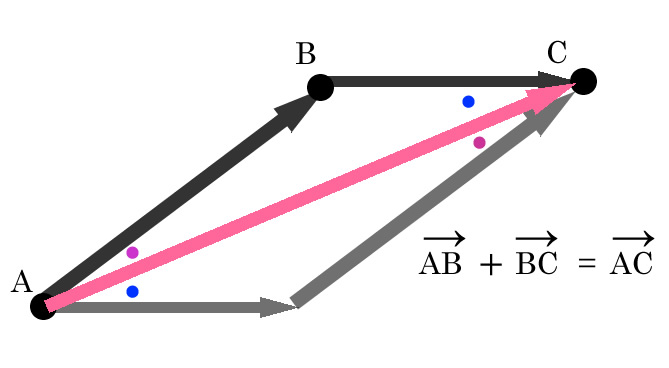 ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 | 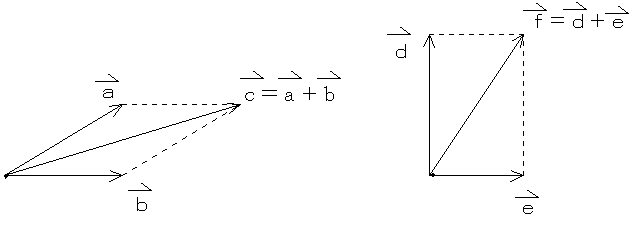 ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 | ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
「平行四辺形 対角線 長さ ベクトル」の画像ギャラリー、詳細は各画像をクリックしてください。
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
 ベクトルの外積と平行四辺形の面積 身勝手な主張 |  ベクトルの外積と平行四辺形の面積 身勝手な主張 |
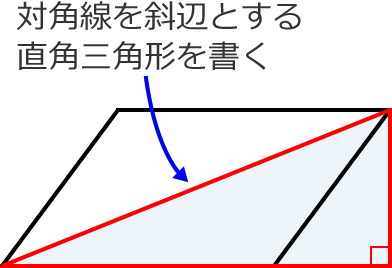
ベクトルとベクトルの和と差、ベクトルと実数との積 二つのベクトルa、bに対して、 図 の(3)のようにa＝,b= と表すとき、有向線分 の表すベクトルcをaとbの和ベクトルまたは合成ベクトルといい、c=abと書く。 これは、b= とも表すとき、OCが平行四辺形OACBの対角線になっていることを意味し 平行四辺形の面積を対角線の長さと角度から求める $2$ つの対角線の長さが $4$ , $6$ 、その2辺のなす角が $60°$ のとき、その平行四辺形の面積を求めよ 対角線は他の対角線の中点で交わるってことを利用して、図にするとこうなるね
コメント
コメントを投稿